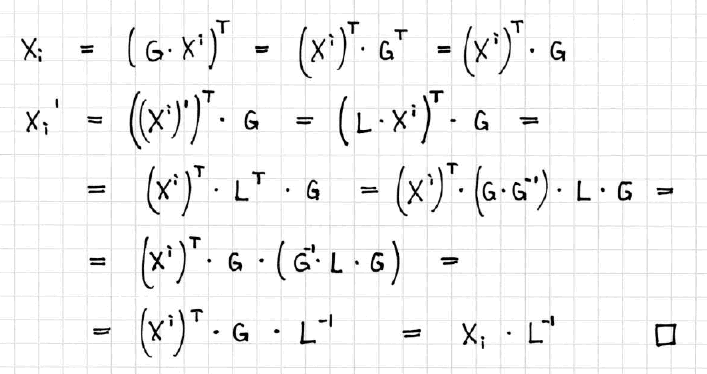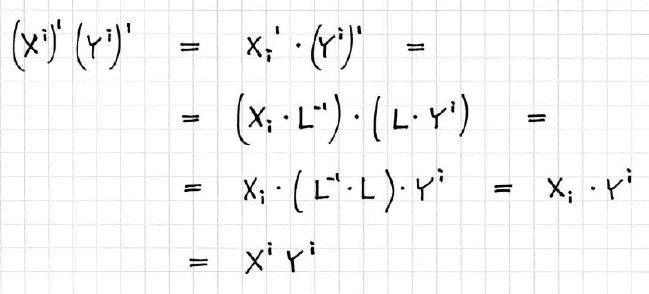M7   Zwei weitere Anwendungen der Matrizenrechnung in der SRT

7.1  Ein Beweis der Transformationsformel für die duale Linarform zu einem Vierervektor

Es gilt

 

 

 

 

 

 

 

 

7.2  Ein Beweis der Lorentz-Invarianz des speziellen Skalarprodukts der SRT

Das Skalarprodukt zweier Vierervektoren Xⁱ und Yⁱ ist definiert durch

 
Das kann leicht durch eine Matrix-Multiplikation ausgedrückt werden:

Mithilfe von 7.1 lässt sich nun leicht zeigen, dass dieses Skalarprodukt ganz allgemein invariant ist unter Lorentz-Transformationen (und daher seinen Namen erst verdient):

 

 

 

 

So einfach geht das mit Matrizenrechnung !

Weitere Anwendungen der Matrizen M und F Es geht noch schöner